LM101-015: How to Build a Machine that Can Learn Anything (The Perceptron)

Multilayer feedforward neural network for binary classification.

Podcast: Play in new window | Download | Embed

Episode Summary:

In this episode we describe how to build a machine that can learn any given pattern of inputs and generate any desired pattern of outputs when it is possible to do so!

Show Notes:

Hello everyone! Welcome to the fifteenth podcast in the podcast series Learning Machines 101. In this series of podcasts my goal is to discuss important concepts of artificial intelligence and machine learning in hopefully an entertaining and educational manner.

In this episode, we discuss the problem of how to build a machine that can learn any given pattern of inputs and generate any desired pattern of outputs when it is possible to do so! It is assumed that the input patterns consists of zeros and ones indicating possibly the presence or absence of a feature. Although we discussed the problem of learning in Episode 2 which was titled “How to Build a Machine that Learns to Play Checkers”, in this Episode we will explore the topic of learning in a little more detail. However, the concepts discussed in this Episode will be helpful for understanding Episode 2 and vice-versa.

In the previous Episode 14, the concept of a McCulloch-Pitts formal neuron was introduced. This is an abstract mathematical model of a brain cell that was developed by the biophysicist Warren McCulloch and the young mathematical genius Walter Pitts in the year 1943. They showed that such a brain cell model (also known as a neuron model) could operate like a logic gate or equivalently an IF-THEN logical rule. By connecting together a group of such computing units where each computing unit corresponded to a desired IF-THEN logical rule, the response of the entire collection of computing units could be combined with an additional computing unit to generate the response generated from the entire group of units. Thus, given a sufficient number of these McCulloch-Pitts formal neurons or equivalently MP-units, one can compute any arbitrary function where each MP-unit essentially generates a response when certain conditions hold. That is, each MP-unit functions as an IF-THEN logical rule. These issues were discussed in detail in Episode 14. Notice this is BEFORE the first digital computer was built! Thus, McCulloch and Pitts essentially invented the concept of a “logic gate” in the quest for understanding how the brain works and today the “logic gate” is a fundamental component common to all digital computers and indeed all “smart machines”!

So, although the concept of being able to REPRESENT any collection of logical rules in an abstract neural network is very exciting, the ability to REPRESENT a collection of logical rules simply means that there exists a way to wire up a collection of this MP-units or computing neurons to realize any collection of logical rules. However, in practice, we often do not know how many rules we need and we do not know which rules we need to solve our computing problems. Ideally, it would be very desirable if one could construct a way for the neural network to learn from experience. One would simply the train the neural network with examples and the system would automatically learn how to connect itself together.

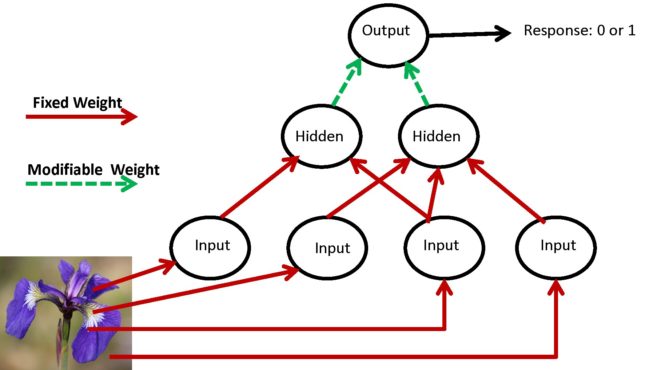
This apparently was the objective of the work of Frank Rosenblatt who was psychologist pursuing research funded by the Air Force Office of Scientific Research in the late 1950s. Frank Rosenblatt’s goal was to develop a network of MP-units which could learn from experience. Rosenblatt called this network The Perceptron. The Perceptron consisted of three distinct groups of MP-units. The first group of MP-units were called the “sensor” or “input units”. The outputs of the first group of MP-units were then connected to the second group of MP-units which were called “association” or “hidden units”. And finally, the outputs of the hidden units were connected to the third group of units which were called “response” or “output units”. The connections from the input units to the hidden units were randomly fixed due to some genetic disposition and not modifiable, while the connections from the hidden units to the output units were modifiable and changed their values depending upon the Perceptron’s experiences.

Although never explicitly stated, Rosenblatt’s intentions for pursuing this architecture are clear. The layered Perceptron architecture should be able to learn arbitrary logical functions if only a small percentage of the hidden units generated responses for specific input patterns over the input units. To increase the chances of randomly obtaining some hidden units with appropriate response patterns, larger numbers of hidden units are included in the network at random with the hopes that some of these hidden units would act like feature detectors which would provide the system with just the right features so that it could solve the desired logic problem.

So the connections from the input units to the hidden units are fixed and have the semantic interpretation of peripheral processing mechanisms that are perhaps genetically determined and which have been optimized via evolutionary processes. In Rosenblatt’s original Perceptorn formulation, the connections from the input units to the hidden units are chosen at random presumably to model the effects of uncertainty due to genetic constraints. The connections from the hidden units to the output units, on the other hand, are allowed to change their values as the Perceptron encounters new experiences in the world. These latter connections were adjusted by a special learning process called the perceptron learning rule. Each input unit, hidden unit, and output unit in the perceptron has a state which is equal to 1 or 0. States with the value of 1 are called “active states”.

The response of the perceptron which corresponds to the output unit’s state is computed as follows. First each hidden unit would compute a weighted sum of the states of the input units and the connection weights for that hidden unit. If that weighted sum exceeded the value of 1, then the response of the hidden unit would be equal to 1 otherwise it would be equal to 0. Next, the output unit computes a weighted sum of the responses of the hidden units and the connection weights of the output unit. If the desired response of the perceptron for that input pattern of states equals the actual response of the perceptron’s output unit, then the connection weights from the hidden units to output units are not adjusted. In this case, we say the input pattern is correctly classified by the perceptron.

If the ACTUAL response of the perceptron for that input pattern of states is LESS than the DESIRED response for the perceptron’s output unit, then the connection weight from an active hidden unit to the output unit is increased by a fixed amount so that the perceptron’s response will be larger in the future. If the actual response of the perceptron for that input pattern of states is GREATER than the DESIRED response for the perceptron’s output unit, then the connection weight from an active hidden unit to the output unit is decreased by a fixed amount so that the perceptron’s response will be smaller in the future. Immediately after each training stimulus is presented, the connection weights of the output units are updated. The training stimuli can be presented to the Perceptron in any order as long each training stimulus is presented a sufficient number of times.

In 1962, Frank Rosenblatt published his famous book titled “Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms” which included the famous Perceptron Learning Theorem. The Perceptron Learning Theorem states that if it is POSSIBLE for the Perceptron to correctly classify all of the input patterns, then EVENTUALLY the Perceptron WILL correctly classify all input patterns. Since we learned in Episode 13 that a Perceptron can always be found which is capable of classifying any set of training data, it follows from the Perceptron Learning Theorem that the Perceptron Learning Rule will eventually learn to correctly classify all input patterns.

Note that a fundamental limitation of the Perceptron Learning Theorem was that it assumes that it is POSSIBLE for the Perceptron correctly classify all of the input patterns. This assumption is not always appropriate. Another fundamental limitation of the Perceptron Learning Theorem is that it is a theorem about memorization rather than generalization. The Perceptron Learning Theorem guarantees the training stimuli will be memorized but does not make any strong claims regarding how it will behave when presented with an input pattern which it had not observed during the training process.

Still, the Perceptron Learning Theorem was an exciting result. Especially at the dawn of the computing age in the year 1958 which was just a few years after the appearance of the first digital computer. Unfortunately, the concept was over sold. In an article published in the July 19, 1958 edition of Science News Letter (https://www.sciencenews.org/) in an article titled “Perceptron” Thinks the Perceptron is described to be a “human being without a life” which can “teach itself to recognize objects”. The article then describes a computer simulation of a Perceptron in which the Perceptron was presented with 100 visual training stimuli consisting of cards. Each card had a square on its left side or its right side. The Perceptron was trained using these 100 stimuli to correctly respond whether the square was on the left side or the right side of the card 97 times out of 100. The article then continues that very soon this device will be able to perform speech recognition and foreign language translation.

In some respects, the scientists were correct. The idea was a powerful and fundamentally important idea which continues to play a central role in modern machine learning algorithms in the twenty-first century. Indeed, the Perceptron is a close cousin of the Support Vector Machine which is a widely used and important algorithm in machine learning. Support Vector machines will be discussed in a future podcast. So the idea that that the Perceptron and its related algorithms would be capable of speech recognition and foreign language translation was in some sense correct but it would take an additional 40 years of scientific research, technology development, and additional advances in artificial intelligence and natural language processing before this dream was realized.

So to summarize, the overselling of the Perceptron was a strategic mistake. Rather than focusing upon the important empirical and theoretical contributions of the Perceptron work, critics tended to focus on the failure of the Perceptron to deliver upon its promises. This is an important lesson for young scientists and engineers even today. Always provide conservative estimates of your ability to deliver scientific advances and scientific technology. In the event that your estimates are too conservative, your customer will be pleasantly surprised!

Continuing with our story at the same time that researchers in artificial intelligence were becoming disillusioned with the concept of Perceptrons, artificial intelligence researchers were discovering the power of rule-based systems of the type discussed in Episode 3 of this podcast series. Artificial intelligence researchers were also realizing the fundamental importance of the role of obtaining the correct representations to support inference and learning in smart machines. Both the concept of “rule-based machines” as well as the concept of “smart representations” of the world play critically important roles in the development and understanding of smart machines and could receive more attention in the early 1970s due to improved access to computing technology for scientific researchers.

These historical forces thus shifted attention away from machine learning algorithms such as the Perceptron in the late 1960s and early 1970s. In 1969, Marvin Minsky and Seymour Papert either intentionally or unintentionally contributed played a major role in amplifying this attentional shift with their book titled “Perceptrons”. The book was intended to be read by someone without a formal background in mathematics but, in fact, the contents of the book required a certain level of maturity in mathematical reasoning. The goal of the book was to provide a realistic appraisal of the computational power of Perceptrons which was done admirably by Minsky and Papert. Unfortunately, however, the book was often misquoted as a book that described the computational limitations of Perceptrons in a pessimistic manner.

Marvin Minsky, in fact, had done important research in artificial neural networks closely related to the Perceptron in his 1954 Princeton Doctoral Dissertation which was titled “Neural nets and the Brain-Model Problem”. I imagine that if you asked Minsky what he thought about Perceptrons in the year 1969 he would say something like: “Perceptrons are an important tool for the artificial intelligence researcher. I’m just concerned that their strengths and limitations are not clearly understood so that’s why we wrote this book.”

Minsky and Papert correctly describe and depict Rosenblatt’s original 1958 conception of the Perceptron as a multi-layer network capable of solving any problem within the first few pages of the book Perceptrons. However, they tend to focus instead upon the limitations of the learning mechanism connecting the hidden units to the output unit. However they say this in a more cryptic way which is less accessible to the general public. Perhaps as a consequence of their analyses in the book Perceptrons, virtually all books on machine learning today incorrectly describe the Perceptron learning algorithm by focusing upon only the connections from the hidden units to the output unit. The idea that the Perceptron was originally proposed as a learning machine with two layers of connection weights tends to be ignored or overlooked. And, instead, most researchers in machine learning describe the Perceptron as a machine learning algorithm consisting of a single McCulloch-Pitts formal neuron output unit whose inputs are directly connected to input units without the addition of any hidden units.

A classic example of a computational limitation of the Perceptron is called the Exclusive-Or problem. Suppose that we have an organism that lives in an environment which has four different types of flowers: large purple flowers, small purple flowers, large yellow flowers, and small yellow flowers. Now, in this environment it turns out that the large purple flowers and small yellow flowers are poisonous and deadly, while the other flowers are excellent sources of nutrition and quite tasty. The learning machine can’t make its decisions by just looking at the color and size of the flower independently. It must take both factors into account. Small flowers can be either poisonous or tasty, while purple flowers can be either poisonous or tasty as well. Suppose the learning machine has two sensors which are McCulloch-Pitts formal neurons. One sensor unit is active when a small flower is present and inactive otherwise. Another sensor unit is active when a purple flower is present and inactive otherwise. Each of the four conditions associated with determining the response of an output unit whose inputs are connected to these two sensor units corresponds to a system of four mathematical inequalities. This system of equations can be shown to be algebraically inconsistent which means that it is IMPOSSIBLE for a single McCulloch-Pitts formal neuron to correctly classify flowers as safe to eat or poisonous. On the other hand, if we add just one hidden unit which becomes active when both sensor units are active and feed the response of that additional hidden unit as an input to the output unit, then the resulting set of inequalities can be shown to be consistent which means that the Perceptron Learning Rule is guaranteed to solve this classification problem if it is presented enough examples. Without that hidden unit, the Perceptron Learning Rule (and any other learning rule) can not learn the required classification solution.

Support Vector Machines have been developed by Vapnik and his colleagues over a time period beginning in the time of the perceptron around the 1960s and continuing today are closely related to the Perceptron Research. Support Vector Machines became especially popular in the Machine Learning community in the mid 1990s and continue to remain very popular. The support vector machine is concept shares many features in common with the classic Perceptron.

The output unit of a support vector machine is a McCulloch-Pitts formal neuron which takes on the values of +1 and -1. The output unit takes on the value of +1 when the weighted sum of its inputs from the hidden units is greater than zero and takes on the value of -1 otherwise. The hidden units are not restricted to be McCulloch-Pitts formal neurons and correspond to the basis functions discussed in Episode 14 of this podcast series. The important innovation of the Support Vector Machine concept is that a computationally efficient method for training the Support Vector Machine was developed in such a way that very robust solutions are obtained. This is achieved by choosing category decision boundaries in such a manner that the members of each category are as far away as possible from those decision boundaries. By choosing the category boundaries in this manner, this introduces a constraint regarding how the learning machine will respond to input patterns that it has never seen before. Versions of the Support Vector Machine have also been developed which seek the best approximating solution in situations when perfect classification by the Support Vector Machine is not possible. Thus, the Support Vector Machine addresses the two limitations of the Perceptron Theory raised previously: (1) the problem of a guarantee of memorization but not generalization, and (2) the problem of learning problems where no solution for entirely correct classification exists.

Another very popular machine learning algorithm is logistic regression modeling which uses a sigmoidal version of the McCulloch-Pitts formal neuron. Sigmoidal functions are discussed in Episode 14 but briefly a sigmoidal function can be viewed as a machine which takes as input a number and returns a number between some minimum value such as 0 and some maximum value such as 1. As the value of the input to the machine increases, the response of the machine becomes larger but the machine’s response is never larger than its maximum value or smaller than its minimum value.

A sigmoidal output unit works by computing a weighted sum of the states of units which are connected to its inputs and the sigmoidal output unit’s connection weights. This weighted sum is called the “support” or “evidence” that the sigmoidal output unit should have a maximal response. As the support increases, the sigmoidal output unit’s response increases. By choosing the maximum value of the response to be 1 and the minimal value of the response to be 0, the sigmoidal output unit response can be interpreted as the learning machines estimated probability that the input pattern belongs to one of two possible categories. The connection weights of the sigmoidal output unit are estimated using the method of maximum likelihood estimation subject to the constraint that the magnitude of the output unit connection weights should be as small as possible. This type of learning procedure can be shown to be a smooth version of the Support Vector Machine approach. The probabilistic interpretation also provides a solid theoretical foundation for understanding and characterizing the performance of a Logistic Regression Machine on stimuli it has never seen before (see Episodes 7 and 8 of this podcast series).

In conclusion, the Perceptron Learning Theorem presented in this podcast in conjunction with the result discussed in Episode 14 that a Perceptron can solve any arbitrary logic problem with enough hidden units, provides a powerful tool for the learning of solutions to a wide variety of machine learning problems. However, it is important to emphasize that the famous Perceptron Learning Theorem has two fundamental limitations: (1) the Perceptron Learning Theorem is only applicable when a correct classification is POSSIBLE, and (2) the Perceptron Learning Theorem is not a theorem about generalization performance.

Although the Perceptron continues to be successfully used in modern machine learning applications and is a great learning algorithm, Support Vector Machine and Logistic Regression Modeling methods are more popular. This is because Support Vector and Logistic Regression methods are more explicitly designed to handle the problem of situations where a classification solution does not exist and the problem of making appropriate inferences for input patterns which have never been observed by the learning machine. Still, despite some important differences, these three learning machines: The Perceptron, The Support Vector Machine, and The Logistic Regression Model are very closely related and equivalent to one another in special cases.

In modern machine learning problems, all three of these methods are frequently used. We will discuss these techniques in greater detail in future episodes of Learning Machines 101.