Gaussian mixture model and multilayer radial basis function machine learning software.

Podcast: Play in new window | Download | Embed

LM101-034: How to Use Nonlinear Machine Learning Software to Make Predictions (Feedforward Perceptrons with Radial Basis Functions)[Rerun]

Episode Summary:

In this episode we describe how to download and use free nonlinear machine learning software which is more advanced than the linear machine software introduced in Episode 13.

Show Notes:

Welcome to the 34th podcast in the podcast series Learning Machines 101 titled “How to Use Nonlinear Machine Learning Software to Make Predictions”. This particular podcast is a RERUN of Episode 20 and describes step by step how to download free software which can be used to make predictions using a feedforward artificial neural network whose hidden units are radial basis functions. This is essentially a nonlinear regression modeling problem. We show the performance of this nonlinear learning machine is substantially better on test data set than the linear learning machine software presented in Episode 13. Basically performance for the linear learning machine was about 13% because the data set was specifically designed to be unlearnable by a linear learning machine, while the performance for the nonlinear machine learning software in this episode is about 70%. Again, I’m a little disappointed that only a few people have downloaded the software and tried things out. You can download windows executable, mac executable, or the MATLAB source code.

Also there is a great website called “deeplearning.net” and if you go to that website and click on “links to software” you will see a large collection of software packages which allow you to implement fairly sophisticated machine learning algorithms. At this point in time, I recommend the software package “Theano” (THEANO) which is a Python library that includes lots of routines to greatly facilitate the development and exploration of various types of deep learning architectures. Regardless of whether you download my software or someone else’s software, it really is important to try out these learning machines and actually see how they work as well as how they fail. This will help you understand this technology in a responsible manner! Ok…let’s begin!!

Hello everyone! Welcome to the twentieth podcast in the podcast series Learning Machines 101. In this series of podcasts my goal is to discuss important concepts of artificial intelligence and machine learning in hopefully an entertaining and educational manner.

In Episode 13, we introduced the linear machine software which can be downloaded for free from the website: www.learningmachines101.com. As discussed in Episode 14, a linear learning machine is limited because there are some problems it will never be able to solve. Episode 14 explains that a multilayer nonlinear learning machine, however, whose inputs feed into hidden units which in turn feed into output units has the potential to learn a much larger class of statistical environments.

In this episode we introduce some advanced nonlinear machine software which is more complex and powerful than the linear machine software introduced in Episode 13. Although the learning machine software introduced in this episode is more powerful than standard linear regression software, it is important to understand that every machine learning algorithm has its strengths and limitations.

In this episode we will explain how to download and use free nonlinear machine learning software which can be downloaded from the website: www.learningmachines101.com. This procedure was discussed in Episode 13 so we just provide a shortened version of the procedure. I encourage you to review Episode 13 if you want additional details. Although we will continue to focus on critical theoretical concepts in machine learning in future episodes, it is always useful to actually experience how these concepts work in practice. For these reasons, from time to time I will include special podcasts like this one which focus on very practical issues associated with downloading and installing machine learning software on your computer. If you follow these instructions, by the end of this episode you will have installed a powerful machine learning algorithm on your computer. You can then use the software to make virtually any kind of prediction you like. However, some of these predictions will be good predictions, while other predictions will be poor predictions.

For this reason, following the discussion in Episode 12 which was concerned with the problem of evaluating generalization performance, we will also discuss how to evaluate what your learning machine has “memorized” and additionally evaluate the ability of your learning machine to “generalize” and make predictions about things that it has never seen before. However, I encourage you to compare the performance of this nonlinear machine software with the linear machine software described in Episode 13. In many cases, you will find the nonlinear machine learning software introduced in this episode is more powerful and capable of learning more difficult problems.

As in Episode 13, we will focus on one of the 298 data sets from the UCI Machine Learning Repository (http://archive.ics.uci.edu/ml/) called the Iris data set which is concerned with the problem of classifying a flower as a member of a flower species based upon physical measurements of the flower. Once you download the software associated with this episode you can explore and evaluate the effectiveness of the nonlinear machine learning software to make predictions on your own data sets. The software is written in the computer programming language MATLAB which is sold by the MATHWORKS (www.mathworks.com). If you have MATLAB installed on your computer, then you can run the software by downloading the source code from this website by running the program “gononlinear.m” which is located inside the folder “nonlinearmachine”. If you do not have MATLAB installed on your computer, then you can still run the software on either a WINDOWS computer or a MAC OS-X computer, but you will need to install the MATLAB function libraries on your computer using a computer program called the MCR Installer. If you have already successfully installed these libraries on your computer to run the software associated with Episode 13, then you do not have to reinstall these libraries. You can just download the executable software directly.

Here is a brief overview of the software installation procedure which is described in great detail in Episode 13. First, obtain the software download password by visiting the website: www.learningmachines101.com . Second, if you have not already done so, install the MATLAB Compiler Runtime Library. If you have already done this installation on your computer as described in Episode 13, then you can skip this step. Third, download either the Windows or the MAC OS-X version of the free software provided under the Apache 2.0 license. The software is downloaded as a ZIP file which you unzip using the software program WINZIP. Make sure you “unzip” this file so that it becomes a standard folder BEFORE you try running the software!

Inside the folder you will find a text file called irisDOC.txt which describes the contents of the data files “testdata.xls” and “trainingdata.xls” which are exactly the same data files used in the linear machine software described in Episode 13. These data files are spreadsheets. Open up the file “testdata.xls” and look at the contents. You will see a spreadsheet which has seven columns of data. Each of the seven columns has a label. The labels of the first two columns are “Setosa” and “Versicolour” which are used to specify three distinct species of the Iris flower: Setosa, Versicolour, and Virginica. Each row of numbers corresponds to the characteristics of a particular Iris flower. So, for example the two numbers in the first row of the file “testdata.xls” are 0 under the category “Setosa” and a 0 under the category label “Versicolour” this pattern of two zeros indicates that the flower belongs to the category Iris Virginica. The second row of numbers has a 0 under the category Setosa and a 1 under the category “Versicolour” indicating that the Iris flower represented by the numbers in the second row correspond to the flower category “Iris Versicolour”. The third row of numbers has a 1 under the category Setosa and a 0 under the category “Versicolour” indicating that the data for the flower specified by the third row of numbers identifies a flower from the species “Iris Setosa”.

In addition, each flower in the database corresponding to each row of numbers in the spreadsheet is characterized by the length and width of its petals as well as the length and width of its sepals. The sepal of a flower is usually a special type of petal or leaf used to protect the flower.The flower represented by the first row of numbers is a member of the species “Iris Virginica” and has a sepal length of 7.7 centimeters, sepal width of 2.8 centimeters, a petal length of 6.7 centimeters, and a petal width of 2 centimeters. The last column is labeled “Intercept” and the purpose of this column will be explained later.

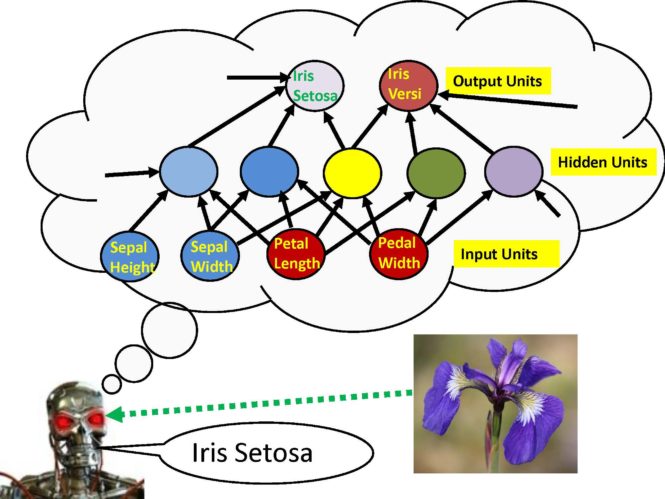
Thus, each row of numbers in the spreadsheet specifies the “inputs” to the prediction machine and the desired “outputs” or “targets” for the prediction machine. In this example, there are five input units (“sepal length”, “sepal width”, “petal length”, “petal width”, “intercept”) and two output units “Iris Setosa” and “Iris Versicolour”. The prediction problem associated with this problem is to use the four features “sepal length”, “sepal width”, “petal length”, and “petal width” in order to predict whether the flower belongs to the species: “Iris Setosa”, “Iris Versicolour”, or “Iris Virginica”.

We consider a special type of prediction machine which we will call the “nonlinear machine”. The nonlinear machine has some variables which is called parameters. Different choices of these parameters lead to different predictions. Specifically, we will generate a number which specifies the “evidence supporting” the hypothesis that the flower species is “Iris Setosa” and we will generate another number which specifies the “evidence supporting” the hypothesis that the flower species is “Iris Versicolour” given that we know specific measurable features of the flower such as the length and width of its petals and the length and width of its sepals.

The architecture of the nonlinear prediction machine consists of three types of computing units which are called the “input units”, the “hidden units”, and the “output units”. When you load a spreadsheet of data into the system, you specify how many targets are associated with the prediction. The number of targets specifies the number of output units. In this problem, the desired response of the prediction machine is the species category which is represented by two targets and hence we have two different output units “Iris Setosa” and “Iris Versicolour”. Each of these output units computes a weighted sum of the outputs of several “hidden units” plus an additional weight which is called the output unit “bias” or “intercept”. The purpose of the “intercept” feature is to provide an additional parameter for learning the average response of the learning machine which is not functionally dependent upon the inputs of the machine whose values vary.

In summary the output unit weights are free parameters of the nonlinear learning machine which it adjusts based upon its experiences with events in its environment. In this case, the “events” correspond to specific training stimuli in the spreadsheet specified as containing the training data.

As previously mentioned, the inputs to each output unit are the hidden unit outputs. These special units are called “hidden units” because they are not input units and they are not output units. Each hidden unit is associated with its own set of free parameters which are called the “hidden unit weights”. The number of hidden unit weights for each hidden unit is equal to the number of inputs to the nonlinear prediction machine where the “hidden unit bias” parameter is defined as the connection weight from a special input unit called the “Intercept unit” to a particular hidden unit. The net input to a hidden unit is computed by first computing the sums of the squares of the differences between each hidden unit parameter and the value of each input unit. Next, the output of a hidden unit is computed by dividing the net input by a number called the “temperature constant” (in the software the temperature is 4) and then plugging the negative value of the resulting number into the exponential function. This type of hidden unit is called a Radial Basis Function and it works like a “feature detector” since input patterns which are close to the hidden unit parameters in a sum of squares difference sense will cause the feature detector or Radial Basis Function to have a stronger response. If the temperature constant is smaller, the response is more specific and the unit is less likely to respond to similar patterns. If the temperature constant is larger the response is less specific and the unit more likely to respond to similar patterns. The temperature constant can either be chosen based upon prior knowledge or learned but in this episode we do not adjust the temperature parameters by the learning process but simply use a fixed value of the temperature parameter and thus refer to this parameter as the temperature constant.

The resulting nonlinear learning machine is thus a type of perceptron or multi-layer feedforward architecture as discussed in Episodes 14 and 15. However, unlike Episode 15, where the input unit to the hidden unit connections are not learnable. In this particular multi-layer feedforward architecture, both the input to hidden unit connections and the hidden unit to output unit connections are adjusted by the learning machine on the basis of its experiences. These adjustments are based upon the method of Gradient Descent which was described in Episode 16. If the connections are adjusted after each presentation of an event, then the learning machine is called an “adaptive learning machine”. If all of the training data is used to adjust the connections among the units at each learning trial, then the learning machine is called a “batch learning machine”. Again, these ideas are discussed in Episode 16.

We begin by focusing upon the case of batch learning. In the batch learning mode, the learning machine first picks the connections from the input to hidden units by randomly picking a training stimulus for each hidden unit and setting the connection weights of that hidden unit so that it will respond strongly to that training stimulus. The connections from the hidden units to the output units are just randomly chosen. Next, the connection weights from the hidden unit outputs to the output unit are adjusted using gradient descent without changing the connections from the input to hidden units. After a certain number of learning trials, the connection weights from the input to hidden units are adjusted using gradient descent without changing the connections from the hidden units to output units. This process is repeated a few times and finally both the connections from the input to hidden units and the connections from the hidden units to output units are adjusted using the training data using gradient descent.

The output of the program reports performance on both the “training data” set and the “test data” set. As discussed in Episode 12, in many applications of machine learning we would like our learning machine to generalize from experience. Thus, it is important that we evaluate the learning machine’s generalization performance. In this episode, we focus upon training the learning machine using a “training data set” and testing it with a “test data set” but more sophisticated methods such as the cross-validation method described in Episode 12 should be used in actual engineering practice.

Ok…at this point…let’s go through the process of actually running the computer program and make sure that the parameters which are input to the program and the output of the computer program has been properly described.

After you execute the program “gononlinear.exe”, a splash screen appears which reviews the licensing agreement. Click ok and then a dialog box will be displayed asking you to identify which variables are the “targets”. The nonlinear learning machine is designed to compute evidence supporting the presence or absence of the targets. If you select the targets “Setosa” and “Versicolour” then the nonlinear learning machine will learn to compute the evidence for the presence of the two targets “Setosa” and “Versicolour” given the petal and sepal length and width measurements in centimeters. Note that in order to select multiple targets you need to hold down the CONTROL key when you make your selection on a WINDOWS operating system. A splash screen confirming your choice of the target variables then appears.

The remaining variables which are presumed to be observable measurements on the flower are called the predictor variables. A splash screen confirming your choice of the predictor variables then appears.

The program then asks you to identify the spreadsheet file which contains the “test data”. It is required that the “test data” file has exactly the same number and type of columns as the “training data” file.

Next the program asks if you want to use a “batch gradient descent” or “adaptive gradient descent”. If you choose “batch gradient descent”, then it will ask you for the magnitude of the initial values of the connection weights which are randomly chosen. This is an important parameter if the initial magnitude of the randomly chosen connection weights is chosen too small, then learning will proceed too slowly. If it is chosen too large, then the system will tend to have difficulty converging to the correct solution. Another parameter is the number of hidden units. Too few hidden units will not be sufficient for the system to learn the problem but if there are too many hidden units then the system will tend to “memorize” the solution and have poor generalization performance. The user also has the opportunity to specify the number of learning trials on this screen.

During the learning process, you will see a screen which has six different windows. The window in the upper-left titled “Objective Function History” plots the “prediction error” as a function of the number of learning trials so you can see how performance improves as a function of learning. The window titled “Objective Function Gradient History” plots a number which measures how rapidly the “prediction error function” is changing at at particular point when the “gradient infinity norm” is close to zero this means that the parameters can’t be adjusted to decrease the prediction error because small changes to the parameter values at this point will not decrease the prediction error. The window titled “Current System State” is a visual representation of the parameter values of the learning machine where each row of color corresponds to a different parameter and the color of that row corresponds to the parameter’s value. The window in the lower-left entitled “Stepsize History” plots how the magnitude of the perturbation to a connection strength changes as a function of the history of learning trials. The window titled “Deviation of Search from Gradient Direction” can be ignored since we are using gradient descent algorithms so the deviation is always zero. And finally, the window in the lower-right hand corner entitled “Prediction Errors” provides a way of visualizing how the prediction errors of the learning machine are changing. Each column of this window corresponds to a different training stimulus and the color of that column indicates how well the learning machine has learned that training stimulus. If the color of a column is a light ocean blue or light ocean green that corresponds to a prediction error of zero. If the color of a column is dark red or dark blue that corresponds to a very poor prediction for that training stimulus.

At the end of the learning process, the performance of the nonlinear machine on both the training data and the test data are reported. Performance of the nonlinear machine may be quite different for the same parameter values for batch learning because the connections from the input to hidden units are randomly initialized with different training stimuli each time the computer program is run. For the default case of 8 hidden units, performance on the training data set is about 80% and performance on the test data set is about 70%. Although this seems low, remember that this training set (as described in Episode 13) was specifically designed to be very difficult to learn. It can be shown, in fact, that this training data set is IMPOSSIBLE for a linear machine to perfectly learn regardless of the choice of learning algorithm. When we tried learning this data set in Episode 13 using the linear learning machine, the linear learning machine’s performance on both the training data and the test data sets was only about 13%!! So the overall performance of the nonlinear machine in this case is substantial.

Still, this does not mean that one should always use the more powerful nonlinear machine. If the problem can be solved with a linear machine, it is preferable to solve it that way since more robust and more efficient methods are available for training linear machines. On the other hand, it’s good to know that technology such as the nonlinear machine described here which more technically might be called either a “feedforward radial basis function” machine or a “Gaussian mixture model” is available for those problems where the linear machine solution is not adequate.

Visit the website: www.learningmachines101.com to not only download the software associated with this podcast so that you can try it out on your own prediction problems but also get references to the machine learning literature which discuss the use of “feedforward multi-layer perceptrons” using Radial Basis function hidden units as well as the closely related work on Gaussian mixture models. These references can be found at the end of the show notes for today’s podcast located at the website: www.learningmachines101.com.

LM101-034: How to Use Nonlinear Machine Learning Software to Make Predictions (Feedforward Perceptrons with Radial Basis Functions)[Rerun]

LM101-034: How to Use Nonlinear Machine Learning Software to Make Predictions (Feedforward Perceptrons with Radial Basis Functions)[Rerun]

Episode Summary:

Show Notes:

Further Reading:

Leave a Reply Cancel reply