Podcast: Play in new window | Download | Embed
Episode Summary:
This particular podcast covers the material in Chapter 2 of my new book “Statistical Machine Learning: A unified framework” with expected publication date May 2020. In this episode we discuss Chapter 2 of my new book, which discusses how to represent knowledge using set theory notation. Chapter 2 is titled “Set Theory for Concept Modeling”.
Show Notes:
Hello everyone! Welcome to the 80th podcast in the podcast series Learning Machines 101. In this series of podcasts my goal is to discuss important concepts of artificial intelligence and machine learning in hopefully an entertaining and educational manner.
This particular podcast is actually the second episode in a new special series of episodes designed to provide commentary of my new forthcoming book. The book’s title is “Statistical Machine Learning: A unified framework” and it will be published by CRC Press in their “Texts in Statistical Science” series in May of this year 2020. The basic idea of the book is that it is designed to provide mathematical tools from the fields of nonlinear optimization theory and mathematical statistics for the analysis and design of machine learning algorithms. You can learn more about my new book by visiting the website: www.statisticalmachinelearning.com.
Each podcast in this special series describes a chapter from my new book. Each podcast is divided into four sections. The first section provides an easy-to-understand self-contained overview of the key concepts from the relevant chapter. The second section is specifically designed to provide guidance to the human student who is using the book for self-study. The third section is designed to provide guidance for the human instructor who is using the book for instruction. The fourth section is designed to provide guidance for robot web spiders (also called web spiderbots or web crawlers) so they can find this podcast and properly index it for humans. But even if you are not a robot web spider…you shouldn’t feel left out! Humans familiar with the relevant terminology will also find this fourth section of the podcast useful for a quick technical overview of what is covered in the book chapter.
This particular episode covers the material in Chapter 2 of my new book titled “Statistical Machine Learning: A unified framework.” Chapter 2 is titled “Set Theory for Concept Modeling”.
[music interlude]
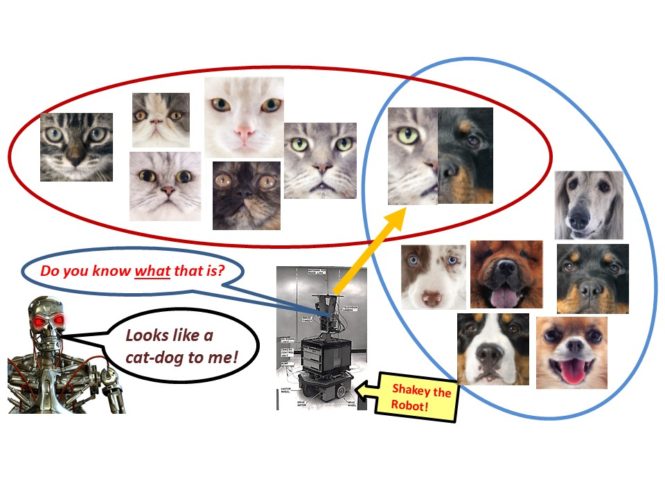
In this episode we discuss Chapter 2 of my forthcoming book, which shows how to represent knowledge using set theory notation. An inference and learning machine must possess representations of the real world. Such representations are mathematical models and thus abstractions of an extremely complicated reality. For example, consider the problem of designing a learning machine capable of distinguishing photographs of dogs from photographs of cats. To achieve this goal, the concept DOG and the concept CAT must somehow be represented in the learning machine yet the variations within and between these species is considerable. A similar challenge is faced in the design of learning machines for processing auditory signals. Two auditory signals specifying how sound pressure varies as a function of time can have a very similar appearance yet correspond to different spoken sentences. Alternatively, two auditory signals which appear quite different could correspond to two different individuals speaking the same sentence.
To address these issues of knowledge representation, it is convenient do define a collection of d feature detectors. Each feature detector returns a different numerical value. Thus, the pattern of d numerical values returned by the d feature detectors is a “feature vector” or equivalently a point in a d-dimensional feature space. The elements of a feature vector are the d feature detectors. A feature detector may be physically measurable (e.g., the intensity of a light stimulus at a particular pixel), abstract (e.g., the presence or absence of a line segment), or very abstract (e.g., happy or unhappy facial expression). Note that it is also possible and quite common to have space-time features which respond to events which occur at particular locations in space over particular regions of time. In summary, the feature vector represents the outcome of a mapping from a set of events in space and time into a point in a finite-dimensional feature space. From a machine learning perspective, this is an absolutely fundamental concept because the starting point of all machine learning algorithms is a method for representing space-time events as feature vectors.
Concept models may be developed within this framework in a straightforward manner. A concept is defined as a subset of the feature space. If a feature vector is a member of this subset, then the feature vector is classified as an instantiation of the DOG concept. Similarly, the concept of CAT would be another subset of this feature space whose elements would correspond to feature vectors specifying different instantiations of cats. In this manner, concepts may be represented using set theory.
If we represent concepts in this manner, it is desirable to have some method of measuring the distance between concepts and feature vectors. This can be achieved by defining a distance function which takes as input two feature vectors and returns a zero if the feature vectors are identical. If the two feature vectors are different, then the distance function returns a positive number which is larger when the two feature vectors are more dissimilar. Different choices of the distance function correspond to different theories of how to measure the similarity between feature vectors. In mathematics, a set of feature vectors combined with a distance function designed to measure feature vector similarity is called a “metric space”.
Furthermore, not only is set theory fundamentally important for machine learning because it allows for the representation of concepts as sets. Set theory is important for machine learning because set theory may be used to represent logical rules and relationships. Logical relationships such as AND correspond to the intersection of two sets. Logical relationships such as OR correspond to the union of two sets.
One very nice feature of this type of representation is that one can construct expressions for representing novel concepts from previously defined concepts. For example, if we have the set of feature vectors representing DOGS and then we have the set of feature vectors whose feature vectors are ANIMALS-WITH-SHORT-LEGS, then the intersection of these two sets is a new concept which is DOGS-WITH-SHORT-LEGS.
The implication or IF-THEN relationship can be reformulated using set theory as well. For example, if the subset of DOGS is contained in the subset of ANIMALS, then one may conclude that every dog is an animal.
Furthermore, since the early beginnings of Artificial Intelligence, the semantic network has played a crucial role in the representation of knowledge. As we will see in a moment, semantic networks are formally represented within set theory as well.
Semantic networks are an important knowledge representation method which play a crucial role in machine learning and mathematics as well.
To illustrate the idea of a semantic network, suppose we want to construct a semantic network with the semantic relation “is a part of”. Using our original photograph image example, we have some regions of the feature space which model the concept of “fingers”, some regions of the feature space which model the concept of “hand”, and some regions of the feature space which model the concept of “body”. The “fingers” are part of the “hand” which, in turn, is part of the body. Using the notation of semantic networks, we draw three circles. One circle which is labeled “hand”, one circle which is labeled “fingers”, and one circle which is labeled “body”. There three circles correspond to three nodes in the semantic network which represent the concepts: “hand”, “fingers”, and “body”. An arrow is drawn from the “body” node to the “hand” node. Then another arrow is drawn from the “hand” node to the “fingers” node. This graphical representation specifies that the finders are part of a hand and that a hand is part of the body.
A second example of a semantic network is a semantic network defined by the semantic relation “is conditionally dependent upon” which plays a role in probabilistic modeling frameworks such as Bayesian Networks and Markov Random Fields. A random variable is a function or feature detector which takes on some value when an event in the environment occurs with some probability. Semantic network representations are also used in probabilistic modeling to specify whether the probability distribution of a particular random variable is functionally dependent upon other random variables. In particular, if the probability distribution of random variable Z is conditionally dependent upon random variable X, then an arc from random variable X to random variable Z is drawn. In summary, the conditional independence semantic network specifies our theory of which space-time events in our statistical environment are statistically independent as well as specifying our theory of the nature of the statistical dependence when particular space-time events are, in fact, correlated.
Now…let’s define the concept of a semantic network more abstractly and study how the concept of a semantic network is related to set theory.
More formally, a semantic network consists of a collection of nodes and a collection of arcs connecting the nodes. In mathematics, this type of representation is called a directed graph. A connection of an arc from the jth node to the ith node typically specifies that node j is semantically related to node i according to the semantic relation R associated with the directed graph. Different semantic relations correspond to different semantic networks. Let the set C be a set of concept nodes. Then an arc from one element of the concept node set C to another element of the concept node set C may be represented as an ordered pair whose first element indicates where the arc originated and whose second element indicates where the arc ended. A semantic network or directed graph is a set of such ordered pairs. Thus, even though a semantic network is often represented in a picture form with circles and arrows connecting the circles, technically a semantic network is simply a set of ordered pairs!
Equivalently, we can rewrite this graphical representation as a collection of ordered pairs. Thus, the nice thing about semantic networks is that they can be drawn as figures so that humans can easily read and interpret them but they can also be represented using the language of set theory without any diagrams at all!
This brings us to the third important reason why set theory is important for machine learning. Although reasoning and learning in environments characterized by uncertainty such as probabilistic environments is a hot area today, we often forget that the majority of the intelligent systems surrounding us today grew out of research associated with representing knowledge using logical rules. This research has been so highly developed and so widely applied that we tend to take it for granted.
Many of the most advanced computer programming languages today as well as algorithms for sifting through information in large databases are based upon the concept of logical rules. Research in Artificial Intelligence possibly beginning with the 1956 Logic Theory Machine developed by Allen Newell and Herbert Simon has made tremendous progress in developing algorithms which can prove theorems automatically. In fact, the computer programming language PROLOG essentially implements an automated theorem prover. You provide PROLOG with a collection of statements and IF-THEN rules and then PROLOG can figure out how to apply the rules to the statements to come to a logical conclusion.
Suppose we have a robot which we want to control. We provide the robot with sensors, image processing systems, auditory processing systems, and so on. Thus, the robot has a collection of feature detectors which can be interpreted as a collection of assertions about its current state and the relation of its current state to its environment. The robot also has a collection of rules which are designed to help the robot execute functions within its environment. For example, an example rule might be: “IF you are located at position X and your goal is to move to position Y, THEN take exactly one step in the direction of position Y.” When you give the robot a command such as “Walk to the Door”, then the robot is essentially proving a mathematical theorem. The proof of the theorem corresponds to a sequence of actions which lead the robot to walk to the door. In practice, this approach doesn’t work too well because I have oversimplified many of the key problems.
On the other hand, the impact of research of this type on the field of Artificial Intelligence has been immeasurable. Indeed, this approach was used in the control systems of Shakey The Robot developed at the Stanford Artificial Intelligence Lab in 1972. On February 2017, the following IEEE Milestone in Electrical Engineering and Computing plaque was presented to the Computer History Museum in Mountain View, California. On the plaque is the following statement:
Stanford Research Institute’s Artificial Intelligence Center developed the world’s first mobile intelligent robot, SHAKEY. It could perceive its surroundings, infer implicit facts from explicit ones, create plans, recover from errors in plan execution, and communicate using ordinary English. SHAKEY’s software architecture, computer vision, and methods for navigation and planning proved seminal in robotics and in the design of web servers, automobiles, factories, video games, and Mars rovers.
In summary, many problems in Artificial Intelligence can be formulated as theorem proving problems. This was a major thrust of research in the 1970s and 1980s and continues to remain an important component of artificial intelligence research as we move forward into the 21st century. There are, of course, fundamental limitations of course to rule-based systems. For example, in many important applications it is impossible to formulate a correct rule. In addition, it is challenging to obtain a set of rules which are sufficient for solving a class of problems of interest yet which are logically consistent. Many of these challenges are now being addressed in the 21st century using statistical machine learning. Still, rule-based artificial intelligence is fundamentally important and widely used, we do not want to throw the baby out with the bath water!!
And, these latter observations lead to the main reason why Chapter 2 is fundamentally so important. Because theorem proving is not ONLY important for developing rule-based systems in machine learning, it is also the essence of all mathematical thought and reasoning. Essentially every machine learning algorithm that exists is described using the language of mathematics and implemented using computer programs. In turn, every computer program is essentially a mathematical model. And finally, all mathematics including probabilistic models, statistical models, and dynamical systems models is based upon the statement of theorems and thus depends upon the mathematical foundations provided by set theory.
The main goal of my new book “Statistical Machine Learning: A Unified Framework” is to provide powerful mathematical tools for the analysis and design of statistical machine learning algorithms. These powerful tools are presented in the form of explicit mathematical theorems with practical verifiable assumptions and practical interpretable conclusions.
Thus, Chapter 2 provides the fundamental mathematical definitions and mathematical tools which are extensively used throughout all of the remaining chapters of the book Statistical Machine Learning: A Unified Framework.
[MUSIC Background]
This section of the podcast is designed to provide guidance for the student whose goal is to read Chapter 2. The contents of Chapter 2 are relatively straightforward so simply reading the chapter from beginning to end is a reasonable strategy. But Chapter 2 contains a lot of information and many different types of definitions. Do not try to memorize the definitions. Instead, the best way to study Chapter 2 is read each definition and try to summarize that definition in your own words and give some examples of the definition. These definitions will be used at later points in the book. Also many of these definitions are indexed in the subject index at the back of the book so if you encounter a term such as “bounded function”, “convex set”, or “open set” when you are struggling through the matrix calculus theory in Chapter 5, you can always go to the back of the book and discover where these terms are defined by using the subject index.
[MUSIC Background]
This section of the podcast is designed to provide guidance to the instructor whose goal is to teach Chapter 2. Remember these notes are available for download by simply visiting this episode on the website: www.learningmachines101.com. In addition, supplemental teaching materials (as they become available) will be available on the website: www.statisticalmachinelearning.com.
Chapter 2 is essentially a quick introduction to topics from elementary real analysis that will be used throughout the remaining 14 chapters of the book. The choice of topics may seem arbitrary but, in fact, they were chosen extremely carefully to quickly provide students with the minimal essential background in elementary real analysis required for the later chapters of the book which delve into matrix calculus, dynamical systems theory, measure theory, and stochastic sequences.
You may want to skip the lecture for Chapter 2, move quickly through the contents of Chapter 2 in lecture, or just cover selected topics in Chapter 2 in lecture and require students to read the remaining topics. When presenting this material in lectures, I provide the formal definition followed by a few examples. Regardless, students should be required to read Chapter 2 and should be tested on its contents possibly using an open book and open notes format to encourage students to understand rather than memorize the definitions in this chapter. Again, the remaining chapters in the textbook frequently make reference to concepts in Chapter 2 so if a definition or concept in Chapter 2 is skipped now it will probably have to be explained later when it arises.
When introducing this chapter to students, I find it useful to start students off with a pep talk regarding why set theory is so fascinating, interesting, important, and relevant to machine learning. A good way to do this is to emphasize that set theory may be interpreted as implementing a theory of concepts in terms of feature vectors, discussing the relationship of set theory to logic, explaining how set theory may be used to represent semantic networks, and of course showing how set theory provides the foundation for the statement of mathematical theorems. The material in this podcast might help in providing some lecture material to help inspire students to study these key concepts in real analysis!!
[MUSICAL INTERLUDE]
This final section is designed mainly for search engines and web spider robots but humans will find this final section relevant also!!
The objective of Chapter 2 is to provide relevant background in elementary real analysis essential for understanding later chapters. It is emphasized that set theory provides a method for developing abstract models of concepts. This is important not only for models of intelligent systems but also for explicitly formulating concepts in mathematics. A variety of important sets are introduced which are required for understanding the discussion in later chapters. These sets include: the set of natural numbers, the set of real numbers, the extended real numbers, countable sets, and the partition of a set. The chapter also emphasizes that a relation between two sets corresponds to a semantic network and may be represented as a graph. A number of important relations and graphs are introduced including: reflexive relations, symmetric relations, transitive relations, complete relations, directed graphs, directed acyclic graphs, undirected graphs, functions, function restrictions, function extensions, and bounded functions. In addition, selected topics about metric spaces are included such as: open sets, closed sets, bounded sets, hyperrectangles, the distance from a point to a set, the neighborhood of a set, and convex sets.
[MUSICAL INTERLUDE]
The book is expected to be available near the end of May 2020 of this year! So get ready!! Get ready!! That’s only 3 months from now!!! I can’t believe it! Indeed, my friends and family were extremely surprised because I have been working on this book for such a long time!!! You can advance purchase the book on the publisher’s website which can be reached by visiting the website: www.statisticalmachinelearning.com. I am also working with my publisher to come up with some discounts for my book for the members of the Learning Machines 101 community so don’t miss out on these discounts!!! Make sure you join the Learning Machines 101 community now so that you are notified when special discounts become available. Discount coupons will be sent directly to your email address!!! Discounts will only be available at particular points in time and announcements of discounts will only be provided to members of the Learning Machines 101 email list.
If you are not a member of the Learning Machines 101 community, you can join the community by visiting our website at: www.learningmachines101.com and you will have the opportunity to update your user profile at that time. This will allow me to keep in touch with you and keep you posted on the release of new podcasts and book discounts. You can update your user profile when you receive the email newsletter by simply clicking on the: “Let us know what you want to hear” link!
In addition, I encourage you to join the Statistical Machine Learning Forum on LINKED-IN. When the book is available, I will be posting information about the book as well as information about book discounts in that forum as well.
And don’t forget to follow us on TWITTER. The twitter handle for Learning Machines 101 is “lm101talk”! Also please visit us on ITUNES and leave a review. You can do this by going to the website: www.learningmachines101.com and then clicking on the ITUNES icon. This will be very helpful to this podcast! Thank you again so much for listening to this podcast and participating as a member of the Learning Machines 101 community!
REFERENCES:
Wikipedia Article on Shakey the Robot.
